용어 정리

• Unconditional DM : ?
• Mode-Collapse : GAN에서, Generator가 다양한 종류의 이미지를 생성하지 않고 한 종류의 이미지만 생성하는 현상
• mode covering behavior
• (DDPM) reweighted object :
• (VQGAN) Quantization
• FID(Frechet Inception Distance) : 실제 이미지와 생성된 이미지에 대해 computer vision 특징에 대한 통계 측면에서 두 그룹이 얼마나 유사한지 즉, 벡터 사이의 거리를 계산하는 메트릭
• Classifier-free Guidance :
• SNR (Signal To Noise Ratio)
  • [계산사진학] Image Restoration - Image Degradation
• 4.3.2 Convolutional Sampling

Abstract

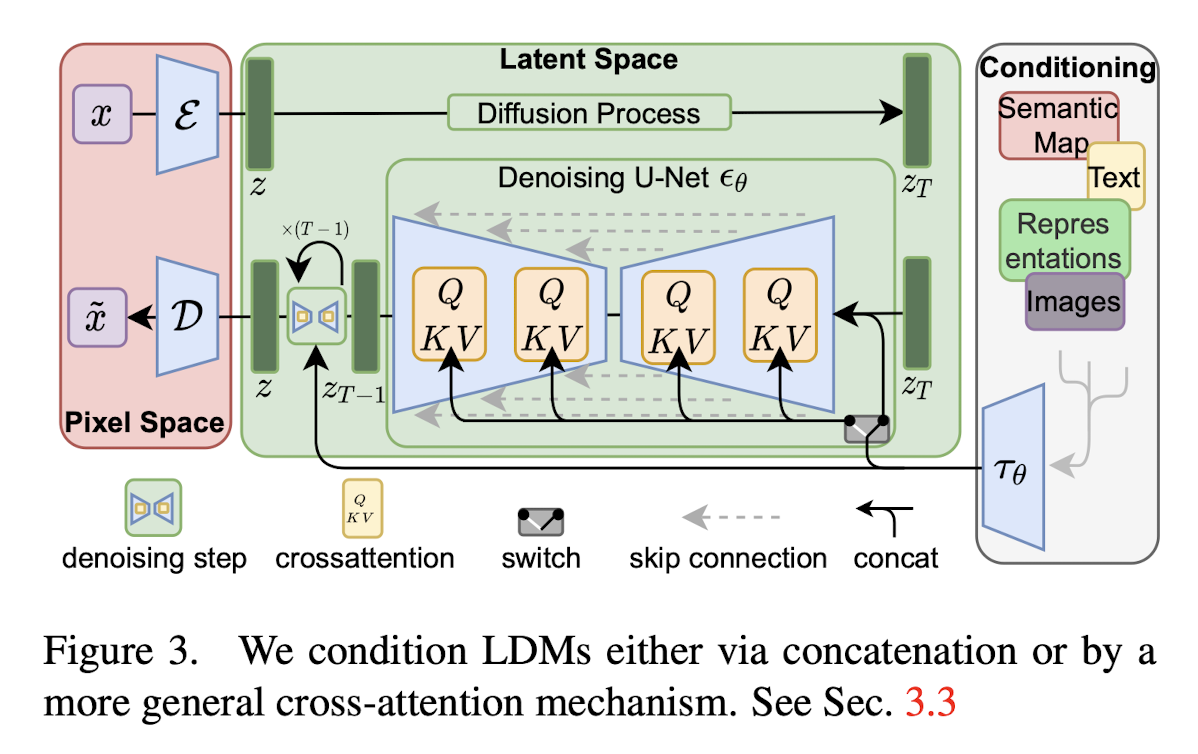
기존의 Diffusion Model들은 Noising / Denoising Process를 Pixel-Wise Space에서 진행했다. 이는 1) 낮은 추론 속도 2) 훈련 시 높은 Computatioinal Cost라는 단점이 있었다. Latent Diffusion Model은 Latent Space 안에서 위의 과정을 진행하는 것으로 하여 위의 문제들을 해결한다. 또한 모델 구조 안에 Cross-attention Layer를 도입해, general conditioning input을 위한 강력하고 유연한 Diffusion 생성 모델을 만들어냄을 보인다.

1. Introduction

• Hight Resolution Image Synthesis of complex, natural scenes
  • 주로 몇십억개의 파라미터를 가진 Auto-Regressive Transformer
  • 유의미한 결과를 냈던 GAN류의 모델들은 굉장히 variablity가 낮은 한정적인 데이터셋에서만 잘 동작
• 최근에는 Diffuision Model들이 굉장히 잘 나감.
  • Class conditional image synthesis, super-resolution 등에서 SOTA 달성
  • Unconditional DM → inpainting, colorization, stroke-based synthesis 등에 적용 가능
• Diffusion Model은 mode-collpase, 학습 불안정 등 GAN의 단점들을 겪지 않으면서도, (파라미터 공유라는 방법에 의해) 몇십억개의 파라미터를 가지는 AR 모델에 필적하는 결과를 보여준다. (매우 복잡한 분포를 가지는 natural image를 잘 표현한다)

2. Related Work

Generative Models for Image Synthesis

• Diffusion Probabilistic Model (DM)
  • Backbone Network인 U-Net이 Image Data에 대한 Inductive Bias를 가짐 → DM의 Generative Power의 기반
• DDPM은 reweighted-objective를 사용
  • 이 경우에 DM은 Lossy Compressor에 대응
  • Image Quality와 Compression Capabilites간의 Trade-Off를 허용
• 그러나 Pixel-Space에서의 평가와 훈련은 여전히 1) 낮은 Inference 속도, 2) 매우 높은 훈련 비용이라는 단점
  • ‘낮은 Inference 속도’는 Advanced Sampling Strategy, Hirearchial Approach를 통해 부분적으로 해결 가능하지만
  • ‘매우 높은 훈련 비용’ 문제 여전히 존재
• Latent Space를 통해 두 문제를 해결하고자 함

3. Method

3.1. Perceptual Image Compression

• Perceptual Compression Model = AutoEncoder = (Trained by) Perceptual Loss + Patch-based Adversarial Objective
  • 이는 Local Realism을 강제하여 Reconstruction이 이미지 집합체에 국한되고, L2나 L1과 같은 Pixel-Space Loss에 의존함으로써 발생하는 blurines를 피할 수 있게 함

• High Variance Latent Space를 피하기 위해 두가지 Regularizationdmf tlfgja
  • KL-reg : learned latent $z$의 standard normal에 대한 KL-penalty
  • VQ-reg : Decoder 안에 Vector Quantizatioin Layer를 사용